
PARLAS DE MANOUNA ORTI
Alzon e la trisesioni de la angulo ·
La retanguli del disco ·
La dupli del cubo ·
La cade sin cade ·
La formula del infinita ·
Un parla de Manouna Orti
Cara sores e frates,
Tra nosa sicle de parlas, nos desveli la trovas xef de la matematiciste Alzon. Sua obras es sola conoseda tra un compila antica, titulida Opera mathematica, scriveda en latina par la monce dom Munius ci ia vive en un monceria ascondeda en la montes rocosa de nosa isola a un tempo distante, en un eda cuando nosa lingua no ia es ancora esistente. Multe manoscritos ia viaja tra la mar, multe ia desapare, ma nosa isola ia recolie obras cuantiosa cual la mundo esterna an no conose; an, per la mundo, algas es considerada como perdeda… per la mundo, ma no per nos!
Oji, me intende revela a vos la construi de un surfas retangulo egal a un surfas sirculo, cual Alzon ia imajina. Acel es multe interesante, car lo nesesa no calcula: per cualce construi jeometrial de esta eda antica, on usa sola un compas – per trasa sirculos, bisesioni un angulo o dupli alga longas –, un regla e un stilo.
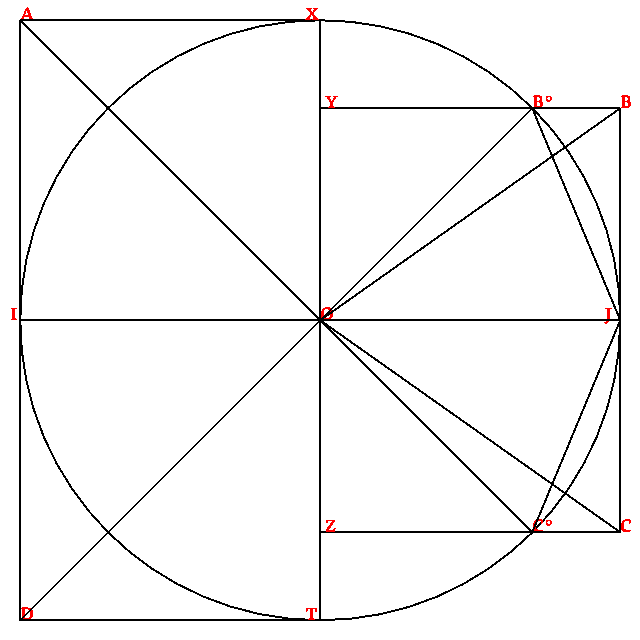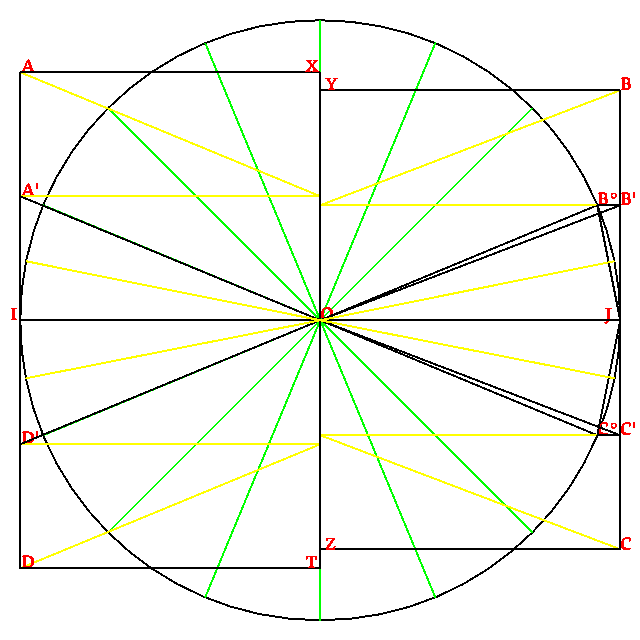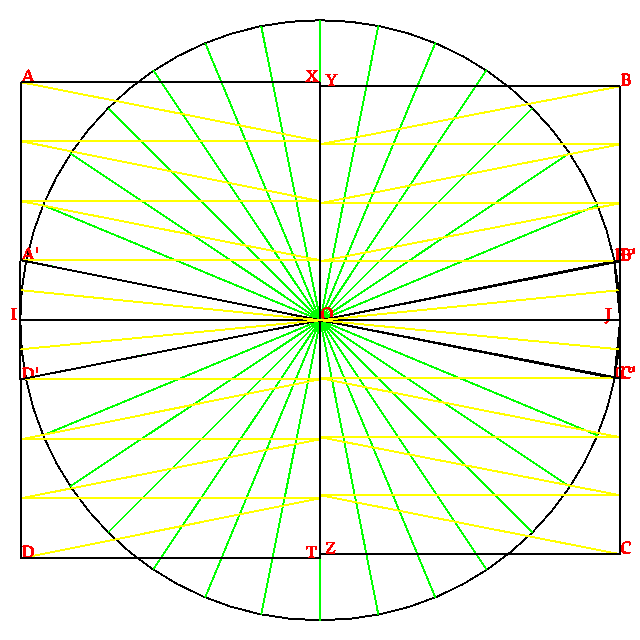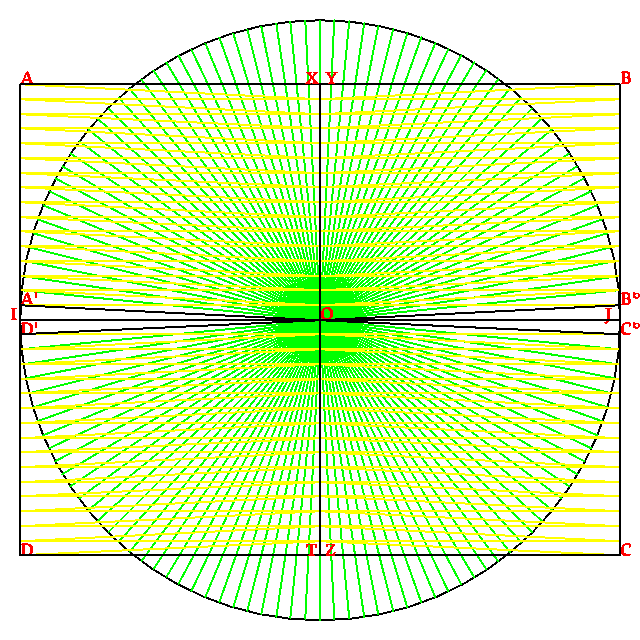
A prima, ta ce nos divide un disco en oto setores egal, con la compas e la regla.
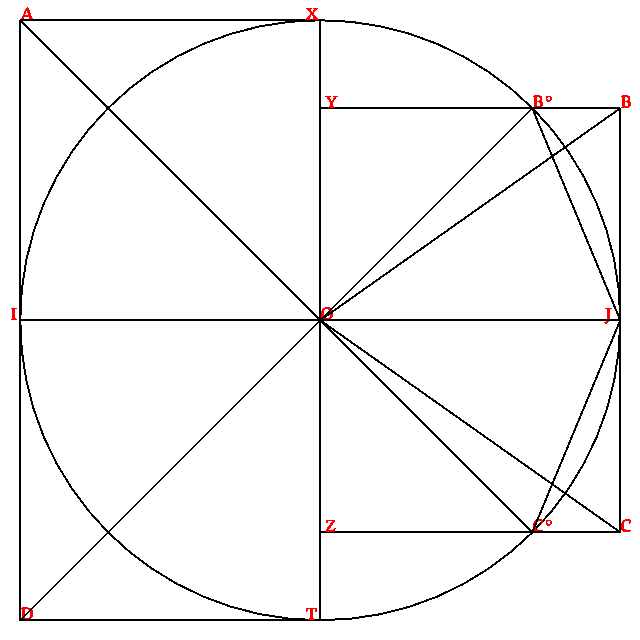
Alzon remente nos de la fato jeometrial demostrada par Euclide, en la libro prima de sua Elementes (en elinica, Στοιχεία), en sua proposa 37: « La triangulos construida sur la mesma basa e entre la mesma paraleles es egal[¹]. » Par acel razona, la triangulo OB°J (a interna de la sirculo) e la triangulo retangulo OBJ, construida sur la mesma basa e entre la mesma paraleles, ave la mesma surfas, cual es inferior a la setor del disco. La retangulo OYBJ, egal a du triangulos interna, es inferior a la cuatri del disco.
Car, a contra, la triangulo IAO es plu vasta ca un setor, la cuadro IAXO, egal a du triangulos de acel tipo, es superior a la cuatri del disco.
Par causa de acel difere, la puntos X e Y es alga separada, tal como la puntos Z e T.
Aora, ta ce nos bisesioni cada setor per formi 16 setores.
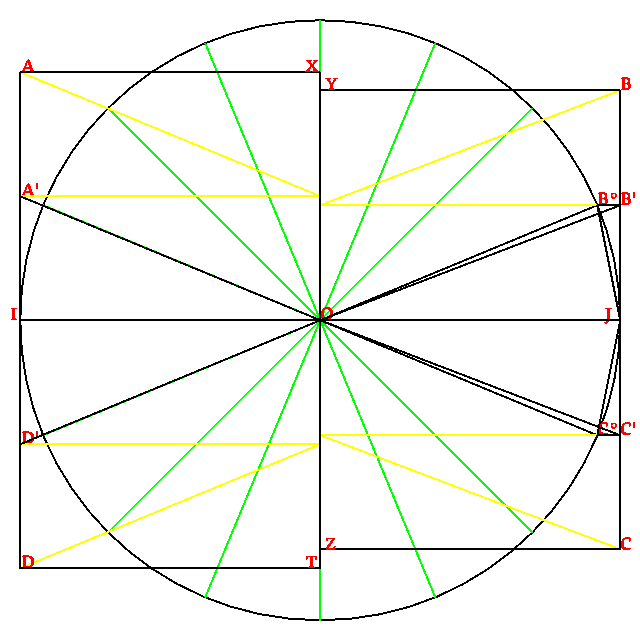
La triangulo OB°J (a interna de la sirculo) es inferior a un setor del disco. La triangulo OB’J, egal a OB°J (con mesma basa e entre mesma paraleles), es inferior a un setor. La retangulo OYBJ, egal a cuatro triangulos OB’J, es inferior a la cuatri del disco.
Car, a contra, la triangulo IA’O es plu vasta ca un setor, la cuadro IAXO, egal a cuatro triangulos de acel tipo, es superior a la cuatri del disco.
Ta ce nos nota ce la difere es min forte ca a la paso 1, e ce la puntos X e Y prosimi a lunlotra, tal como la puntos Z e T.
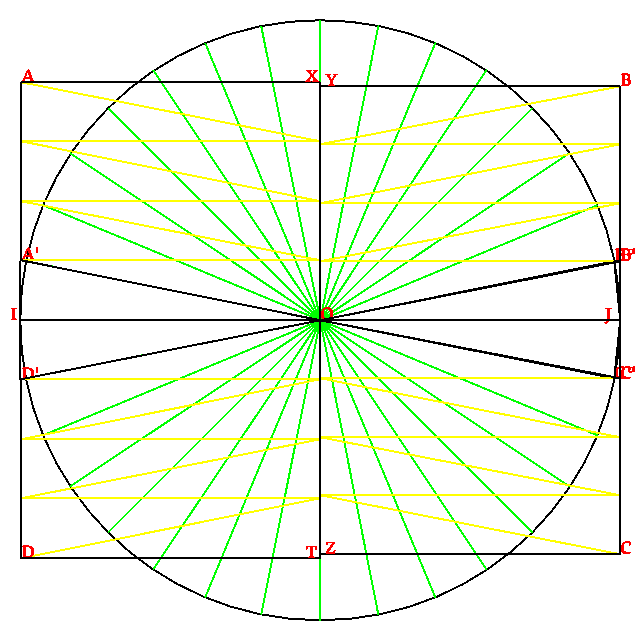
A cada ves, nos bisesioni la setores de la disco. Los dupli en cuantia, e nos debe dupli la cuantia de triangulos per formi la retangulos IAXO e OYBJ.
A sinistra, la retangulo IAXO diminua pico e pico, en ce a destra, la retangulo OYBJ aumenta sua surfas pico e pico.
La puntos X e Y prosimi plu e plu, como la puntos Z e T.
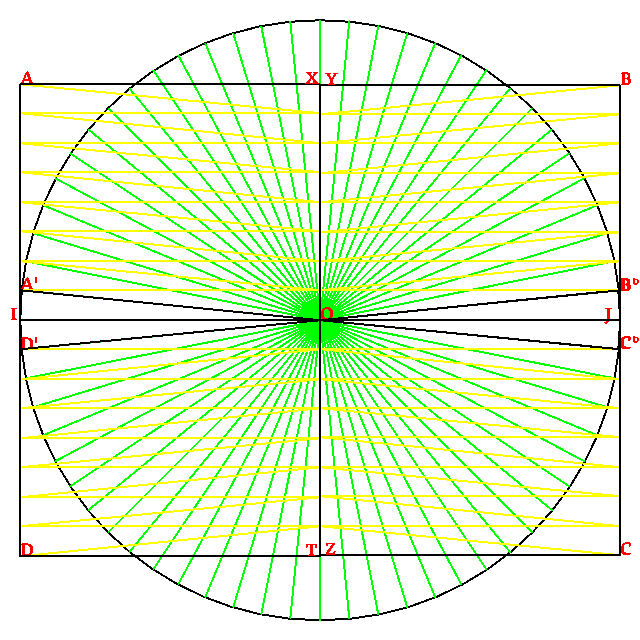
Cuando la distantia XY (o ZT) es plu streta ca la punta de la stilo, en tal modo ce la puntos A, X, Y, B apare aliniada (tal como la puntos C, Z, T, D), la prosede fini, e on ia trasa un retangulo ABCD con un surfas egal a la surfas del disco.
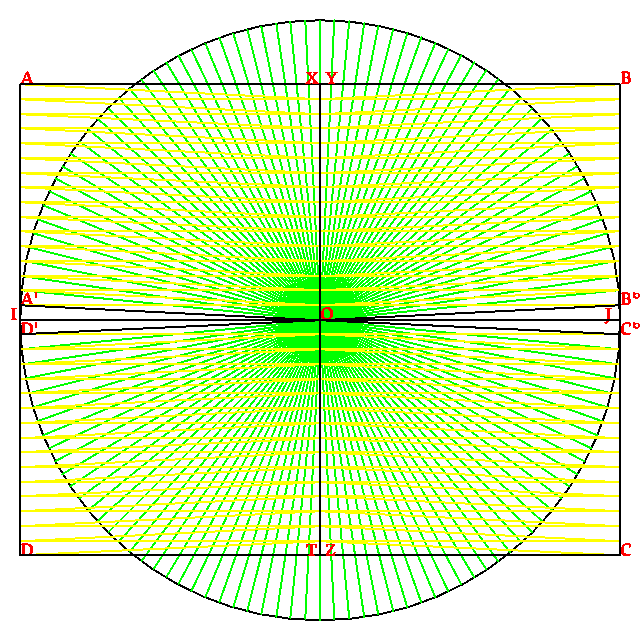
Acel on ia debe fa.
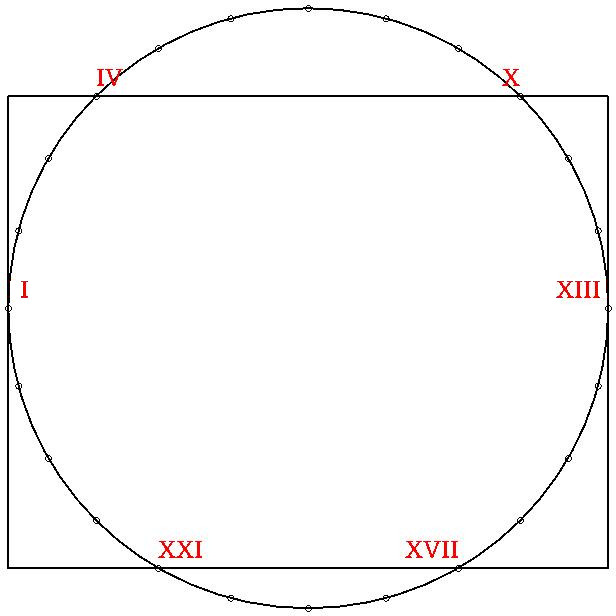
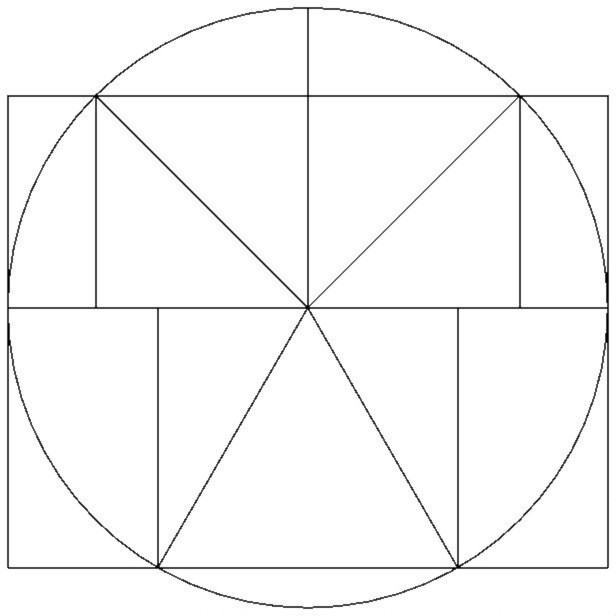
Per conclui sua article, dom Munius presenta du figures jeometrial supraponable, con esta descrive: « Pone sur un sirculo dudes cuatro puntos ecuidistante. Condui un linia tra la puntos 4 e 10. Condui un linia tra la puntos 17 e 21. Sur acel linias paralel, fa un retangulo pasante tra la puntos 1 e 13. La surfases de esta retangulo e de acel sirculo es cuasi simil[²]», e esta nota corta: « Acel desinias es un aprosimi comun de la construi de Alzon.» An si dom Munius scrive ce acel figur es “comun”, nos suposa ce el mesma es sua creor – per acel causa, nos nomi lo “la retangulo de Munius” –, e, donce, ce el es la descovror, par la ajunta de la radis cuadral de 2 a la radis cuadral de 3, de un aprosimi de π.
Sores e frates onorable, me ia parla.
[¹] Euclide, Elementes, I, 37: « La triangulos construida sur la mesma basa e entre la mesma paraleles es egal.» 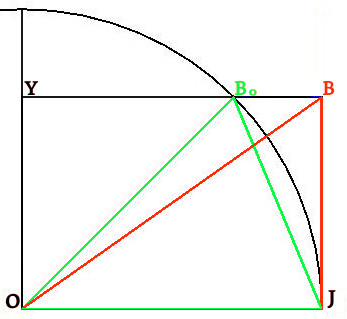
[²] In circulo, XXIV puncta aequidistantia pone. Duc lineam per puncta IV et X. Duc lineam per puncta XVII et XXI. Quibus super lineis parallelis, age rectangulum per puncta I et XIII. Areae istius rectanguli et illius circuli pares paene sunt inter se.
Esta paje es presentada con la lisensa CC Attribution-Share Alike 4.0 International.
Lo ia es automata jenerada de la paje corespondente en la Vici de Elefen a 9 desembre 2025 (09:50 UTC).